ホタル百科事典/ホタルに関する調査研究レポート
東京都のゲンジボタル生息地においては、保全に関して多くの問題を抱えており、絶滅が危惧されている場所も少なくない。しかしながら、生息地において50年後、100年後に個体群はどのような数に変動するのか、あるいは絶滅の可能性はどのくらいあるのか、といった個体群の存続可能性の検討は全く行われていない。一般的に、絶滅のリスクを高める要因としては、個体数が少なくなると確実に生存率や繁殖率を低下させる決定論的要因と、偶然性が個体群の動態を強く支配するようになる確率論的要因に分けられる。確率論的要因は、数が少なくなるにしたがい偶然が個体群の運命を大きく支配するようになることにより生じるため、絶滅確率や存続可能個体数等について数理モデルによる予測も容易である。そこで、今回、東京都青梅市A地区における個体群動態( Population dynamics )の数理モデルを用いたコンピューター・シミュレーションに基づく個体群存続可能性分析( Population Viability Analysis, PVA )により、ゲンジボタルの存続可能性の評価と絶滅確率、最小存続可能個体数の推定を行った。
2003年から対象地で実施した調査と人工飼育データを基に、生活史からゲンジボタルの個体群動態モデルを構築した。今回用いた個体群動態モデルは、行列モデル(matrix model)である。行列モデルとは、”行列”式によって個体数の経時的変化を表現するモデルである。
このモデルは、様々な年齢サイズやサイズ段階に分けられる個体で構成され、年齢やサイズに依存する繁殖率や死亡率(生存率)をもつ種の個体数変化を表現するのに適している。そこで、まず生存率と繁殖率に基づきゲンジボタルの生活史を以下のように区分した。
ステージ |
項目 |
|---|---|
成虫 |
メスの個体数 |
卵 |
卵数 |
幼虫(1〜2齢) |
孵化した幼虫数 |
留まる幼虫数 | |
死亡数 | |
次段階への数 | |
幼虫(3〜4齢) |
留まる幼虫数 |
死亡数 | |
次段階への数 | |
幼虫(5〜終齢) |
留まる幼虫数 |
死亡数 | |
上陸数 | |
蛹 |
死亡数 |
成虫 |
羽化数 |
死亡数 | |
産卵可能なメスの個体数 |
このように、いくつかの生育段階に区分した時、ある生育段階から次の生育段階へ推移する確率を「推移確率」と呼ぶ。これら生育段階について、それぞれ推移確率(生存率)や繁殖率を求めると、これを行列の形で表すことができる。これを「推移行列」と呼ぶ。推移行列を用いると、各生育段階に属する個体数がある年(t)から、その翌年(t+1)にかけて、どのように変化するのかを予測することができ、また推移行列の固有値や固有ベクトルから個体群増加率や内的自然増加率(Intrinsic rate of Natural increase)、年齢構成(安定齢分布)を知ることができ、現在の個体群構造の安定性を評価することができる。
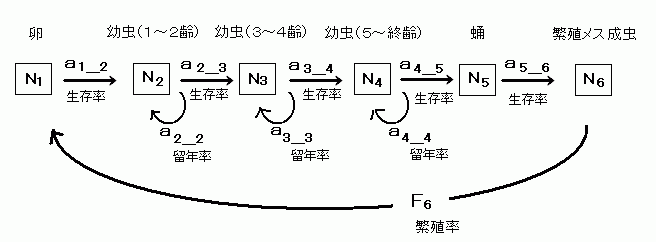
図1.ゲンジボタルの生育段階に基づく行列モデルの概念図
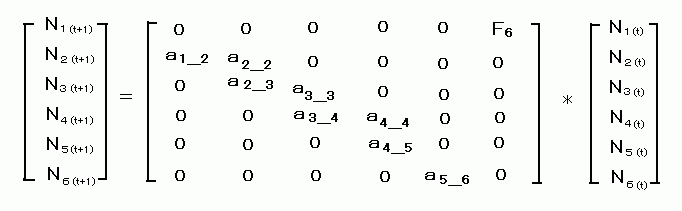
図2.レフコビッチ行列モデル
ゲンジボタルの生育段階に基づく推移行列モデル中のパラメータは、2003年〜2008年の現地調査データ(東京都青梅市A地区)を基本にし、現地では不明確な部分は1977年〜1978年と2002年〜2003年に行った人工飼育のデータから補完し算出した。推移行列の各行列要素の算出は、表1.の基準で分類し、それぞれの平均値を用いた。また、羽化成虫の雌雄比率は1:1とし、産卵可能なメスの生存率を0.489として繁殖率を求めた。
0 |
0 |
0 |
0 |
0 |
163 |
0.891 |
0.331 |
0 |
0 |
0 |
0 |
0 |
0.231 |
0.306 |
0 |
0 |
0 |
0 |
0 |
0.176 |
0.209 |
0 |
0 |
0 |
0 |
0 |
0.092 |
0 |
0 |
0 |
0 |
0 |
0 |
0.343 |
0.489 |
個体群の増加率(λ)は、齢別生存率(lx)と齢別繁殖率(mx)が分かれば下記の式から求めることができる。![]()
表2の推移行列の最大固有値(λ)=個体群増加率を計算すると、1.0034028 、最大固有値の自然対数である固有ベクトル( r )=内的自然増加率 0.00339702 となり、一年間に0.34%の僅かながら増加傾向にあることがわかる。しかしながら、これは指数曲線になって個体数は増加し続ける。現実は、そこに生活できる個体数には上限があると見るのが自然であり、個体数が多くなると、その増加にブレーキがかかるものと想像される。つまり、
という性質を持つ。こうした個体群の成長曲線(S字状曲線:個体群密度増大に伴い環境抵抗によって増加率が低下し、環境収容力Kに達すると安定化する)はロジスティック曲線と呼ばれ、以下の微分方程式(ロジスティクス方程式)で示される。
dN/dt = r(1-N/K)N ・・・( r = 内的自然増加率、N = 個体数、t = 時間、K
= 環境収容力) この解を変数分解で解くと![]() 左辺を部分分数に分解してから積分すると
左辺を部分分数に分解してから積分すると![]() と表される。
と表される。
自然環境下では台風による増水で幼虫の生存率が下がったり、カワニナの減少による成長不良で留年率が上がったりするなど、環境の変化(変動)で推移確率も変動する。例えば、台風による増水が10年おきに2年連続して起こったと仮定すると、ゲンジボタル成虫の発生は以下のグラフ1が示すように、62年後には絶滅してしまう。あるいは、周期的にカワニナ生息数が増減したと仮定すると、グラフ2のようにゲンジボタル成虫の発生数は絶滅することなく増減を繰り返す。
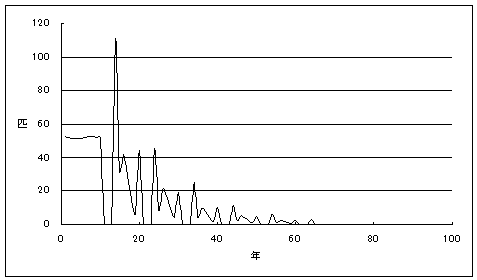
グラフ1.増水被害によるゲンジボタル成虫の個体群動態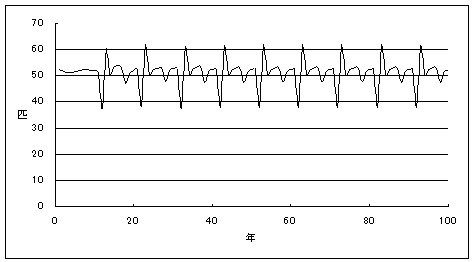
グラフ2.カワニナの増減によるゲンジボタル成虫の個体群動態
ゲンジボタルの生息地では、様々な環境変動が複合的に起こっており、これら環境変動を行列モデルに取り入れる方法の1つとして、推移行列モデル中のパラメータを変動させる方法(確率変動性)を用いた。まず、成虫の初期個体群サイズ N6(t)を適当に与え、その個体群が安定年齢分布にあると仮定し各ステージの個体数を計算で求めた。そして、環境条件が非周期的で相関していない状態で変動するという仮定をおき、カワニナの減少や増水などの影響を受けやすい幼虫時期3ステージの生存率と留年率を変動させた。生存率と留年率は、arcsin 変換を行い正規近似した後、各々平均値と標準偏差を求め正規分布を仮定して乱数値を発生させ、その年の各パラメータの値として翌年のそれぞれのステージの個体数を予測した。
行列計算の値は、100回(100年)分計算し、これを500回繰り返し、50年後のゲンジボタル個体群(成虫)の個体数予測のシュミレーションを行った。そのうち個体群が絶滅した回数(卵、幼虫、蛹、成虫すべてが0になり、その後も0の状態が続いた場合)を求め、全体の繰り返し数で割った値を絶滅確率とした。通常、個体群存続可能性分析(Population Viability Analysis, PVA)では、予測を100年後に設定する場合が多いが、予測がより遠い将来であればあるほど、個体数の変動に影響する不確定要因も増加するため、推定の信頼性が低くなる。よって近い将来の推定にとどめるべきと判断し、50年後に設定した。
安定環境における個体群は、初期個体数に関わらず50年後に絶滅することはないが、個体群動態モデルに確率変動性を組み入れると、初期個体群サイズN(t)の値によっては絶滅する場合が出てくる。それは、環境の確率変動性によって幼虫の生存率や留年率が年変動し、それによって繁殖個体群サイズが大きく振動し、振動の大きさによっては個体数が0になってしまう場合が生じるからである。
今回、個体群動態モデルに用いた生活史パラメータのうち、絶滅確率(extinction probability) に与える影響が最も大きいパラメータとして幼虫期に対して環境変動を与えたが、その確率変動の大きさ(標準偏差)によっても絶滅確率が大きく変動する。正確な最小存続可能個体数の予想には、生存率と留年率の平均値と標準偏差の精度を高めることが必要であるが、本シュミレーションでは、以下の平均値、標準偏差を用い、3つの初期個体群サイズについてシミュレーションを行った。(グラフ3)
平均値 |
標準偏差 |
|
a2_2 |
0.331 |
0.088 |
a2_3 |
0.238 |
0.127 |
a3_3 |
0.306 |
0.334 |
a3_4 |
0.176 |
0.117 |
a4_4 |
0.209 |
0.148 |
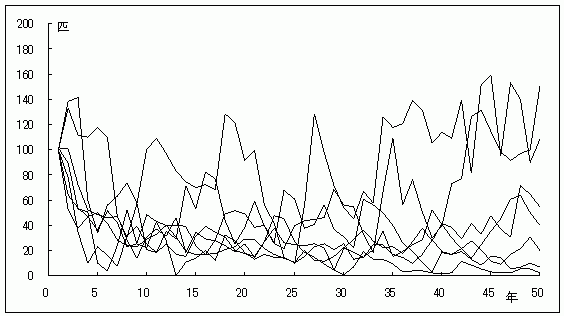
グラフ3.ゲンジボタルの個体群動態(初期値100匹)
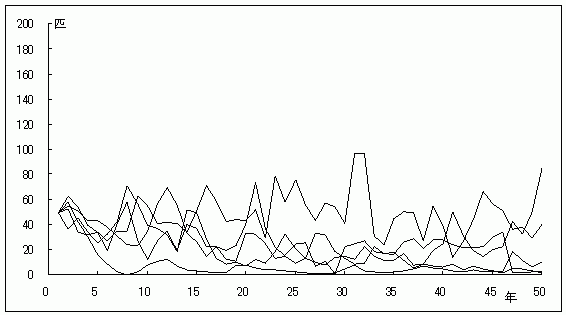
グラフ4.ゲンジボタルの個体群動態(初期値50匹)
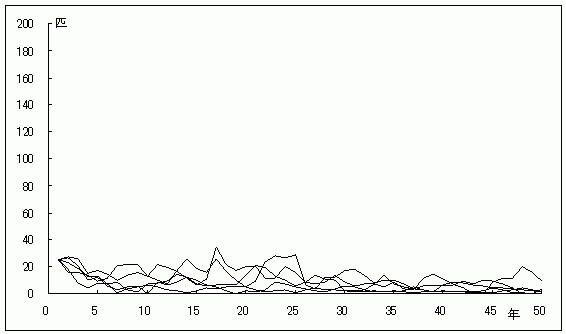
グラフ5.ゲンジボタルの個体群動態(初期値25匹)
初期個体群サイズが25匹の場合、50年後の絶滅確率は4%で、早ければ20年後に絶滅する可能性がある。初期個体群サイズが大きくなれば絶滅確率も低くなり、50匹では絶滅確率は0.5%で、100匹を越えると0.1%になった。
個体群の動態モデルの場合、密度依存性や環境収容力(環境容量)(carrying capacity)を組み入れるのが適切である。ホタルの場合、環境収容力は成虫ではなく、幼虫の数に対して適応するのが適切であると考えられる。上記の環境収容力を組み入れない計算では、幼虫の数がとてつもなく大きな数値になり、個体群も際限なく増加するケースもシミュレーション結果に出てきてしまう。しかしながら、環境収容力の質を問うためには、カワニナやその食べ物となる珪藻類など低次生産過程の取り込みとその動態を考慮した個体群動態に対するより詳細な予測が必要とされ、河川生態系全体のモデルを構築する必要があるため、本モデルでは環境収容力を1〜2齢幼虫を50,000匹、3〜4齢幼虫を30,000匹、5〜終齢幼虫を20,000匹、合計100,000匹と仮定して、表3のパラメータの平均値と標準偏差を用い計算した。
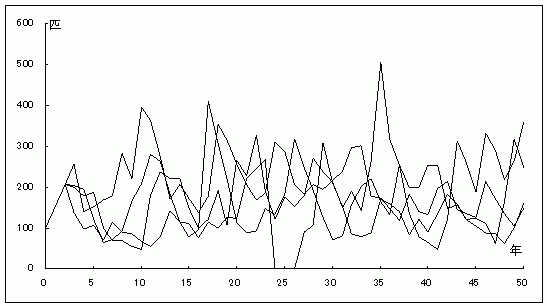
グラフ6.ゲンジボタルの個体群動態
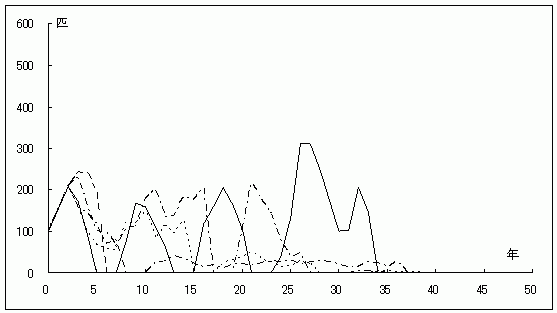
グラフ7.ゲンジボタルの個体群動態(絶滅型)
コンピューター・シミュレーションの結果、環境収容力を組み入れない場合(グラフ3)と比べて絶滅確率が大きくなり、初期値100匹でも50年後の絶滅確率は5%になり、早ければ6年後に絶滅する場合もあった。
ゲンジボタルの最小存続可能個体数 ( Minimal Viable Population,MVP )は、環境収容力を組み入れた場合で50年後に95%の確率で存続している最小個体数とすると、東京都青梅市A地区では、およそ100匹になる。ただし、この数値はあくまでも数理モデルの確率論的結果による。最小存続可能個体数と存続確率の関係は、下のグラフ8のようになる。
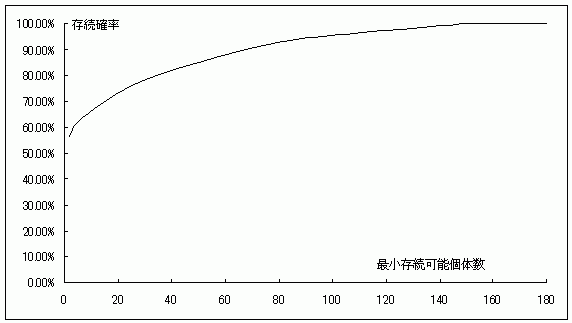
グラフ8.ゲンジボタルの最小存続可能個体数と50年後の存続確率
ゲンジボタルの個体群動態モデルに用いた生活史パラメーターのうち、内的自然増加率( r )に与える影響が大きいものはどれなのかを検証した。ゲンジボタル幼虫の生存率と成虫の繁殖率をそれぞれ平均値を中心に増減させた時の内的自然増加率を求めると、強い相関関係にあり、パラメーターの値が大きくなれば大きな内的自然増加率が得られた。成虫の繁殖率では、1.0ポイント毎に内的自然増加率がおよそ0.0014ポイント増減する(グラフ9)が、幼虫の生存率では成虫の繁殖率に比べて傾きが大きい。また、1〜2齢、3〜4齢、5〜終齢幼虫といったステージが進む毎に傾きが大きくなった。(グラフ10)
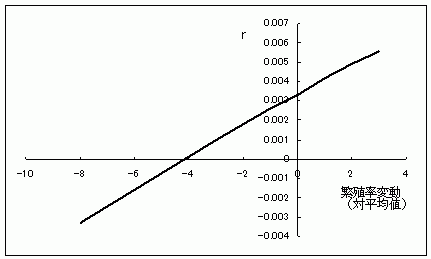
グラフ9.ゲンジボタル成虫の繁殖率と内的自然増加率
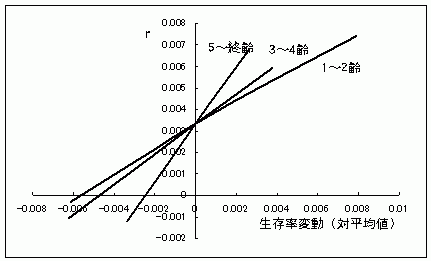
グラフ10.ゲンジボタル幼虫の生存率と内的自然増加率
以上のことから、ゲンジボタル成虫の繁殖率は、それほど内的自然増加率に影響を与えていないことが分かる。しかし、幼虫の生存率では、僅か0.001ポイントの増減で内的自然増加率が変化し、5〜終齢幼虫に至っては平均値よりも0.0024ポイント低下しただけで、個体群は減少傾向に向かうことが分かった。つまり、終齢幼虫の生存率が個体群の増減に大きく影響していると言えるが、水中で数年かけて大きく育ち、後は上陸して蛹になろうという幼虫の生存率が下がれば個体群が減少するのは当然である。
内的自然増加率は、環境的影響を受けない増殖率(マルサス係数)であるから、そこで、ゲンジボタル幼虫(5〜終齢)の生存率の変動と50年後の絶滅確率の関係をコンピューター・シミュレーションにより分析した。生存率パラメーターは、確率変動の大きさ(標準偏差)を変えて調べた。この時、他のパラメーターの値は一定にし、初期値は成虫を100匹とした。標準偏差の大きさは、変動幅 0.001 から、0.1 までの値を用いた。結果は(グラフ11.12)、変動幅が
0.001 と 0.01 の場合はおよそ250匹前後を中心に推移し、絶滅することはない。一方、変動幅 0.1 の場合は、50年後の絶滅確率は14%で、1年後より様々な個体数の変動があり、早ければ10年後に絶滅するケースもあった。
5〜終齢幼虫の生存率に影響を与える環境変動を考えると、大雨などの増水での幼虫の流失等が考えられるが、カワニナの減少や水質悪化等により継続的に若齢幼虫の生存率低下も加われば、(グラフ13)のように個体数は減少の一途をたどり、50年後の絶滅確率は20%、80年後には100%となってしまう。
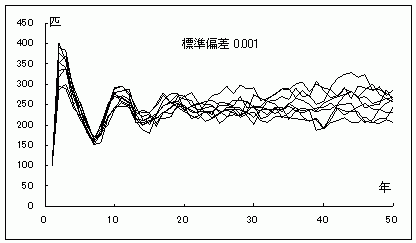
グラフ11.ゲンジボタル幼虫(5〜終齢)の生存率と個体群動態
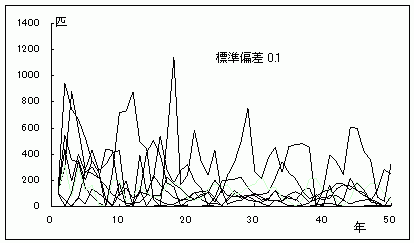
グラフ12.ゲンジボタル幼虫(5〜終齢)の生存率と個体群動態
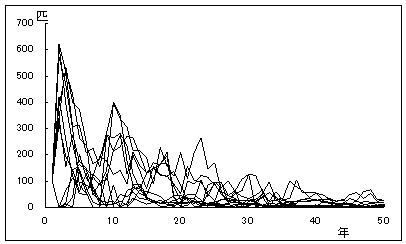
グラフ13.ゲンジボタル幼虫の生存率と個体群動態
今回の数理モデルを用いた個体群存続可能性分析の結果から、ゲンジボタルの生態に関する注目すべきことが確認できた。グラフ3やグラフ6から分かるように、ある年では発生が0になるが、その翌年は再び発生するという点である。これは、絶滅したわけではなく、ゲンジボタルは留年する幼虫がおり、1年で成虫になる場合と2年、もしくは3年以上かかって成虫になる場合があることによる。(グラフ14)
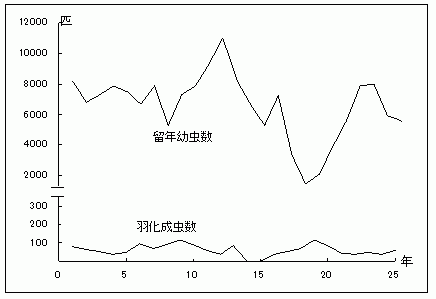
グラフ14.ゲンジボタルの発生数と留年幼虫数
1年で卵から成虫になる場合は、羽化成虫数が0になればその地区での個体群は絶滅と言える。しかし、ゲンジボタルでは、羽化成虫が0で産卵数、孵化幼虫とも0であっても、様々なサイズの留年幼虫が生息している。ゲンジボタルは、カワニナの繁殖や生息数とは関係なく留年する幼虫がおり、水害時でも小さい幼虫ほど生存率も高い。また、成虫の羽化数が少なくても、数年かけて成虫になる留年幼虫の存在により、近親交配を避け遺伝的多様性も保っている。こうした生態的特徴がゲンジボタルの種の保存戦略となっており、不安定で変動が大きい環境において個体群が高密度に達していない状態で適応度を高め、内的自然増加率を最大化させる
戦略( r 戦略 )の1つであると言える。
しかしながら、相対的に個体数が少ない場合は、絶滅は免れてもほそぼそと生き延びているという状況で、大きな環境変動が起これば、一気に絶滅してしまう可能性があると言える。また、いったん、個体群サイズが小さくなると、遺伝的浮動、近交弱勢、確率論的変動など、さらに集団サイズを低めようとする要因が働くことにより、絶滅への進行が加速する場合もある。或いは大きな個体群でも幼虫が死んでしまうような環境変化(水質悪化や開発等)が起これば、絶滅の可能性がある。
東京都青梅市A地区のゲンジボタル生息地では、ここ数年、発生ピーク時でおよそ100〜200個体の飛翔が確認できているから、発生の総個体数は500以上であると推定できる。今回の結果からは、台風などによる増水で、幼虫やカワニナが大量に被害を受けなければ、絶滅する危険性は極めて低いと言える。しかしながら、分析にあたっては、幼虫の生存率や留年率などのパラメータを生息地で計測することは不可能であり、そのため人工飼育のデータを代入せざるを得なかった。また、環境変動には、人為的な開発による被害や乱獲などは含まれていない。更には、環境収容力については仮定値を用いた。生息環境にはそれぞれ個体群が維持できる最大の個体群サイズがあり、個体密度が増加すれば、個体群成長率は減少することが予想される。例えば幼虫の留年率(成熟度)を見ると、人工飼育下では密度とも関係があり、カワニナの数と関係なく高密度ほど留年率や死亡率が高くなる。また、また、最小存続可能個体数が数値上およそ100匹であっても、実際は短期間にまとまって発生しなければ、配偶行動を行えず、更には小集団が長期間続けば近親交配が起こり、繁殖率の低下や病気への抵抗力低下などの影響で、結果として絶滅する可能性が高い(アリー効果)。
こうしたことから、今回の分析結果の信憑性は高いとは言えない。実際は、東京都青梅市A地区における最小存続可能個体数は、100匹より遙かに多いと考えられるし、絶滅確率も高いと思われる。より正確な分析を進めるためには、各パラメータは生息地の地域性や特殊性も考慮する必要がある。詳細な現地データの集積が不可欠である。また、ロジスティックモデルを変形して、個体群密度が低い時や環境収容力を超える個体群密度の時には、負の個体群成長率となるように定式化する方法で、アリー効果を入れた個体群動態モデルを構築する必要もある。今後、更に詳しい分析を行えば、各ゲンジボタル生息地における現状と問題点、保全方法の検討ができるであろう。
昨今、ホタルの保全方法として一般的に行われている、終齢幼虫の放流は、一見個体群の減少を防ぎ、ホタル再生に向けた解決策と思われがちだが、個体群動態の各パラメータを詳細に分析し、ホタル減少の原因やその要因を明らかにした上で対策を立てることが大切であって、安易な幼虫放流は、ゲンジボタルの存続可能性には結びつかない。各々の生息地で分析を行えば、絶滅確率を高める原因が蛹の生存率(羽化率)にあるかもしれない。或いは成虫の繁殖率にある場合もある。幼虫の放流だけを続けても、幼虫が蛹になる場所や成虫が飛び回る暗い空間、交尾、産卵できる環境がなければ、個体群は存続しない。
関連記事
参考及び引用文献、資料
BACK[ホタルの初見日に関する考察] NEXT[ヘイケボタルの個体群動態解析及び存続可能性分析]
ホタルと美しい自然環境を守りましょう。 / Copyright (C) 2001-2025 Yoshihito Furukawa All Rights Reserved.